За достижения, которые сначала вызывают смех, а затем – раздумья
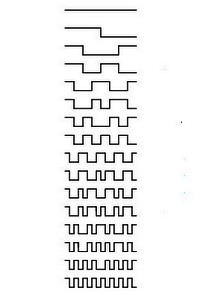 Первые 16 функций Уолша | Автомобиль Алкоголь Вера
Война Волосы Врачи
Геометрия Дети Женщины
Животные Запах Звук
Здоровье Кино Кладбище
Книга Космос Кофе Кошка
Лицо Мозг Мужчины
Музей Насекомые Общество Пенис
Предметы Продукты Психология
Птицы Разное Растения Секс Собака
Спорт Суд Техника Туалет
Финансы Цвет Экскременты /Реклама/ Шнобелевская премия - архив Двоичная последовательность чашек кофеРоберт М. Ричман, (Robert M. Richman), Мэрилендский университет в Колледж-Парке (University of Maryland, College Park), Эммитсберг, США, опубликовал статью "Рекурсивные двоичные разностные последовательности" (Recursive Binary Sequences of Differences), в журнале "Комплексные системы" (Complex Systems), 2001, 13,381–392. В работе исследуется подмножество функций Уолша (Walsh functions), изучаются их свойства и даются алгоритмы, которые генерируют функции. Функциями Уолша называется семейство функций, принимающих значения только +1 и -1 на всей области определения, как выключатель - или включен, или выключен. Каждая функция разделяется на два интервала и индексируется целым числом n. Показано, что функция может быть использована для генерации n-й производной, и важность этого иллюстрируется для решения класса задач минимизации. К примеру, проблемы кофейника. В кофейнике существует градиент концентрации ароматизатора: в процессе заваривания концентрация кофе уменьшается, так что кофе крепче на дне кофейника, чем сверху. Завихрение производит горизонтальную, а не вертикальную конвекцию, поэтому оно не устраняет градиент концентрации. Возникает вопрос, как наполнить из кофейника две чашки кофе A и B одинакового объема, чтобы получить одинаковую концентрацию кофе в этих двух чашках? Один кофейник. Две чашки A и B. Обозначение AB является двоичной последовательностью из двух вариантов - верхняя половина кофейника наливается в чашку А, затем нижняя половина в чашку B. Если у вас есть терпение сделать четыре налива одинакового объема, возможными последовательностями выливания являются AABB, ABBA и ABAB. Если вы хотите еще больше уменьшить разницу между чашками и имеете еще больше терпения, можно сделать восемь наливов одинакового объема, по четыре в каждой чашке. Число возможных последовательностей теперь составляет 35. Оптимальной последовательностью будет ABBABAAB. С еще и еще большим терпением можно сделать 16 наливов, по восемь в каждую чашку. Число возможных последовательностей заливки - 6435. Оптимальная последовательность ABBABAABBAABABBA. И так далее. Этот результат может быть применим и к более важным, чем кофе, проблемам. Например, часто трудно равномерно распределять пигмент красителя в краске. Но возникает естественный вопрос, как правильно налить три чашки кофе?
 Источник - пресса |
| (c) 2010-2024 Шнобелевская премия | ig-nobel@mail.ru |

