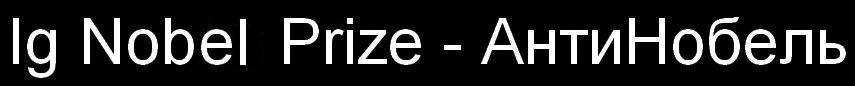
За достижения, которые сначала вызывают смех, а затем – раздумья
 Канзас плоский | Автомобиль Алкоголь Вера
Война Волосы Врачи
Геометрия Дети Женщины
Животные Запах Звук
Здоровье Кино Кладбище
Книга Космос Кофе Кошка
Лицо Мозг Мужчины
Музей Музыка Насекомые Общество Пенис
Предметы Продукты Психология
Птицы Разное Растения Секс Собака
Спорт Суд Техника Туалет
Финансы Цвет Экскременты /Реклама/ Шнобелевская премия - архив Канзас такой же плоский как блинМарк Фонстад, Уильям Пугач, кафедра географии, Государственный университет Техаса, Сан-Марко, Техас и Брэндон Фогт, кафедра географии, университет штата Аризона, Темпе, штат Аризона. В этом отчете мы применили основные научные методы для того, чтобы ответить на вопрос "Канзас такой же плоский как блин?" 
Рис.1. (a) хорошо приготовленный блин; и (b) , штат Канзас [1]. Во время движения по американскому среднему Западу, часто приходится слышать замечания путешественников, что “этот штат плоский, как блин". Авторы данного изречения, кажется, качественно зафиксировали некоторые характеристики топографо-геодезической разведки [2]. Этот простой вопрос – "насколько плоский блин?" - пробудил наш аналитический интерес, и мы отправились отыскивать "плоскости" обоих, блина и конкретного штата Канзас. Технический подход к блинам и Канзасу Невозможность приобретения как Канзаса размером с блин, так и блина размером с Канзас, вынуждает прибегнуть к математическим методам, для того чтобы сделать точное сравнение. Одним из общих показателей меры "плоскости" в геодезии является коэффициент "сглаживания". Длина эллипса, большая полуось a, сравнивается с его малой полуосью b, используя формулу сглаживания, f = (a - b) / a. Идеально ровная поверхность будет иметь сглаживание f = 1, тогда как эллипсоид с одинаковыми осями не будет иметь сглаживания вовсе, и f станет равно нулю. Например, наша земля немного сплюснута у полюсов из-за своего вращения, что делает ее большую полуось несколько длиннее, чем ее малая полуось, давая общий коэффициент сглаживания f = 0.00335. Для обоих, Канзаса и блина, мы апроксиммировали поперечные сечения локальных эллипсоидов полиномиальными уравнениями второго порядка. Эти полиномиальные уравнения позволили нам оценить большие и малые полуоси локальных эллипсоидов и, таким образом, мы можем упрощенно вычислить меру сглаживания f. Материалы и Методы Мы купили хорошо приготовленный блин в местном ресторане "Международный дом блинов", и как можно быстро, пока тот не высох, приготовили его для анализа путем отделения образца в виде узкой полоски 2-см шириной. Мы получили топографию макро-блина посредством цифровой обработки изображения блина и линейки на калибровочной шкале (см. Рис.2). 
Рис.2. Оцифрованная поверхность поперечного сечения блина. Мы сделали еще один топографический профиль для сравнения с помощью софокусной лазерной микроскопии. Важность этого исследования требовала, чтобы мы следовали правилу "Ни есть, ни пить", пока не добьемся своего. Соответствующий знак размещался в микроскопной комнате на самом видном месте. Микроскоп показывает одну точку возвышения на каждые 10 мм и имеет максимальную поверхность диаметром 2 см (см. Рис.3). 
Рис.3. При просмотре в масштабе 50 мм, блин выглядит более труднопроходимым, чем большой Каньон. Мы измеряли западно-восточный профиль Канзаса, взятый из цифровой модели рельефа (ЦМР) масштаба 1:250 000 геологической службы Соединенных Штатов. В общем, расстояние между соседними точками возвышенности на разрезе ландшафта было примерно 90 метров. Мы добывали разрезы поверхности и оценки плоскости из цифровых моделей рельефа Канзаса и блина, используя географическую информационную систему. Результаты Топографические разрезы, как Канзаса, так и блина, на миллиметровом масштабе оба довольно плоские, но этот первичный анализ показал, что Канзас, несомненно, более плоский (см. Рис.4). 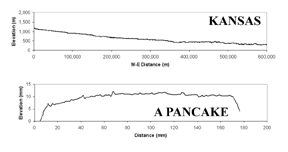
Рис.4. Топография поверхности Канзаса и блина. Математически, значение 1,000 будет соответствовать идеальной плоскости. Расчетная плоскость для цифрового изображения разреза блина составляет величину примерно 0.957, которая является довольно плоской, но далеко не идеально плоской. Софокусное лазерное сканирование показало, что поверхность блина еще более неровная. Измерения плоскостности Канзаса представило для нас большую проблему, чем измерения плоскостности блина. Штат оказался настолько плоским, что программное обеспечение выдало предельно возможное значение плоскости f = 1. Эта величина слишком хороша, чтобы быть правдой, так что мы сделали более сложный анализ, и после многих часов утомительной работы по совершенствованию программного обеспечения смогли оценить, что величина плоскости Канзаса составляет примерно 0.9997. Строго математически степень его плоскости может быть описана как "чертова равнина". Заключение Проще говоря, наши результаты показывают, что Канзас значительно более ровный чем блин. Примечания 1. Фотография Канзаса в районе Вичита, штат Канзас. Это может иметь значение, потому что город Либеральный, Канзас проводит ежегодный фестиваль "Международный день блина". 2. Чтобы подчеркнуть междисциплинарное значение нашей работы, мы должны также упомянуть, что в последнее время некоторые сообразительные космологи, после проведения детальных измерений реликтового излучения, также описали вселенную следующим образом - "плоская, как блин".
Источник - пресса |
| (c) 2010-2026 Шнобелевская премия | ig-nobel@mail.ru |

